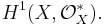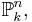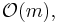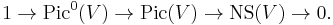Picard group
In mathematics, the Picard group of a ringed space X, denoted by 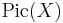 , is the group of isomorphism classes of invertible sheaves (or line bundles) on X, with the group operation being tensor product. This construction is a global version of the construction of the divisor class group, or ideal class group, and is much used in algebraic geometry and the theory of complex manifolds.
, is the group of isomorphism classes of invertible sheaves (or line bundles) on X, with the group operation being tensor product. This construction is a global version of the construction of the divisor class group, or ideal class group, and is much used in algebraic geometry and the theory of complex manifolds.
Alternatively, the Picard group can be defined as the sheaf cohomology group
For integral schemes the Picard group can be shown to be isomorphic to the class group of Cartier divisors. For complex manifolds the exponential sheaf sequence gives basic information on the Picard group.
Contents |
Examples
The name is in honour of Charles Émile Picard's theories, in particular of divisors on algebraic surfaces.
The Picard group of the spectrum of a Dedekind domain is its ideal class group.
The invertible sheaves on projective space
for  a field, are the twisting sheaves
a field, are the twisting sheaves
so the Picard group of 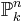 is isomorphic to
is isomorphic to  . The Picard group of the affine line with two origins over
. The Picard group of the affine line with two origins over  is isomorphic to
is isomorphic to 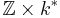 .
.
Picard scheme
The construction of a scheme structure on (representable functor version of) the Picard group, the Picard scheme, is an important step in algebraic geometry, in particular in the duality theory of abelian varieties. It was constructed by Grothendieck (1961/62), and also described by Mumford (1966) and Kleiman (2005). The Picard variety is dual to the Albanese variety of classical algebraic geometry.
In the cases of most importance to classical algebraic geometry, for a complete variety V that is non-singular, the connected component of the identity in the Picard scheme is an abelian variety written Pic0(V). In the particular case where V is a curve, this neutral component is the Jacobian variety of V.
The quotient Pic(V)/Pic0(V) is a finitely-generated abelian group denoted NS(V), the Néron–Severi group of V. In other words the Picard group fits into an exact sequence
The fact that the rank is finite is Francesco Severi's theorem of the base; the rank is the Picard number of V, often denoted ρ(V). Geometrically NS(V) describes the algebraic equivalence classes of divisors on V; that is, using a stronger, non-linear equivalence relation in place of linear equivalence of divisors, the classification becomes amenable to discrete invariants. Algebraic equivalence is closely related to numerical equivalence, an essentially topological classification by intersection numbers.
See also
References
- Grothendieck, A. (1961/62), V. Les schémas de Picard. Théorèmes d'existence, Séminaire Bourbaki, t. 14,, http://www.numdam.org/item?id=SB_1961-1962__7__143_0
- Grothendieck, A. (1961/62), VI. Les schémas de Picard. Propriétés générales, Séminaire Bourbaki, t. 14,, http://www.numdam.org/item?id=SB_1961-1962__7__221_0
- Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR0463157, OCLC 13348052
- Kleiman, Steven L. (2005), "The Picard scheme", Fundamental algebraic geometry, Math. Surveys Monogr., 123, Providence, R.I.: American Mathematical Society, pp. 235–321, arXiv:math/0504020, MR2223410
- Mumford, David (1966), Lectures on Curves on an Algebraic Surface, Annals of Mathematics Studies, 59, Princeton University Press, ISBN 978-0-691-07993-6, MR0209285, OCLC 171541070
- Mumford, David (1970), Abelian varieties, Oxford: Oxford University Press, ISBN 978-0-19-560528-0, OCLC 138290